AI has cracked a key mathematical puzzle for understanding our world
Unless you’re a physicist or an engineer, there really isn’t much reason for you to know about partial differential equations. I know. After years of poring over them in undergrad while studying mechanical engineering, I’ve never used them since in the real world.
But partial differential equations, or PDEs, are also kind of magical. They’re a category of math equations that are really good at describing change over space and time, and thus very handy for describing the physical phenomena in our universe. They can be used to model everything from planetary orbits to plate tectonics to the air turbulence that disturbs a flight, which in turn allows us to do practical things like predict seismic activity and design safe planes.
The catch is PDEs are notoriously hard to solve. And here, the meaning of “solve” is perhaps best illustrated by an example. Say you are trying to simulate air turbulence to test a new plane design. There is a known PDE called Navier-Stokes that is used to describe the motion of any fluid. “Solving” Navier-Stokes allows you to take a snapshot of the air’s motion (a.k.a. wind conditions) at any point in time and model how it will continue to move, or how it was moving before.
These calculations are highly complex and computationally intensive, which is why disciplines that use a lot of PDEs often rely on supercomputers to do the math. It’s also why the AI field has taken a special interest in these equations. If we could use deep learning to speed up the process of solving them, it could do a whole lot of good for scientific inquiry and engineering.
Now researchers at Caltech have introduced a new deep-learning technique for solving PDEs that is dramatically more accurate than deep-learning methods developed previously. It’s also much more generalizable, capable of solving entire families of PDEs—such as the Navier-Stokes equation for any type of fluid—without needing retraining. Finally, it is 1,000 times faster than traditional mathematical formulas, which would ease our reliance on supercomputers and increase our computational capacity to model even bigger problems. That’s right. Bring it on.
Hammer time
Before we dive into how the researchers did this, let’s first appreciate the results. In the gif below, you can see an impressive demonstration. The first column shows two snapshots of a fluid’s motion; the second shows how the fluid continued to move in real life; and the third shows how the neural network predicted the fluid would move. It basically looks identical to the second.
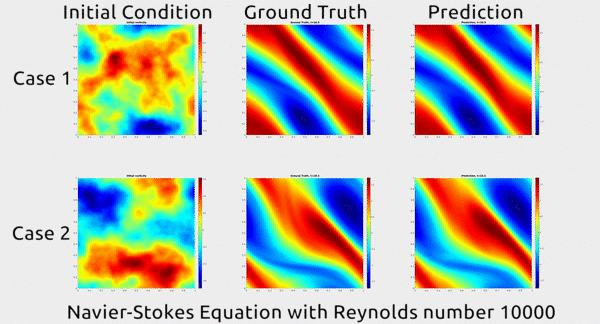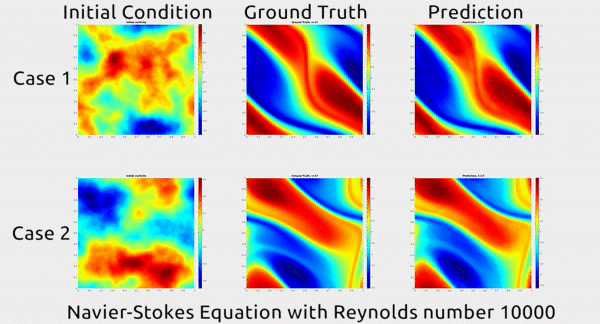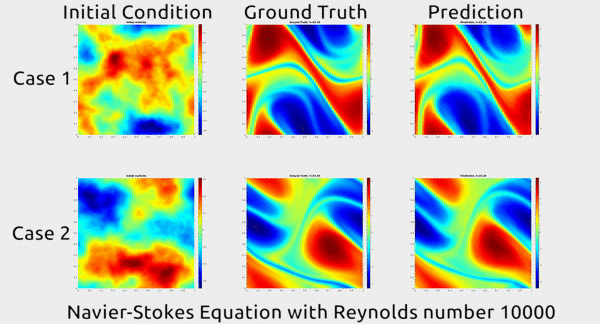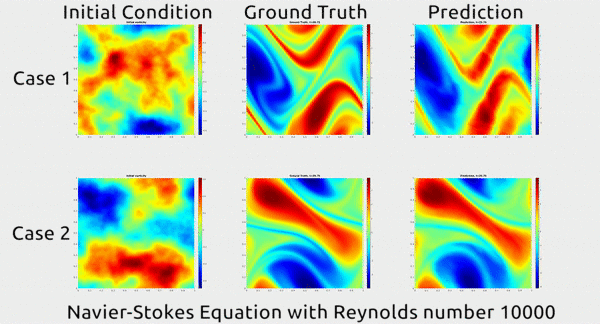
The paper has gotten a lot of buzz on Twitter, and even a shout-out from rapper MC Hammer. Yes, really.
Okay, back to how they did it.
When the function fits
The first thing to understand here is that neural networks are fundamentally function approximators. (Say what?) When they’re training on a data set of paired inputs and outputs, they’re actually calculating the function, or series of math operations, that will transpose one into the other. Think about building a cat detector. You’re training the neural network by feeding it lots of images of cats and things that are not cats (the inputs) and labeling each group with a 1 or 0, respectively (the outputs). The neural network then looks for the best function that can convert each image of a cat into a 1 and each image of everything else into a 0. That’s how it can look at a new image and tell you whether or not it’s a cat. It’s using the function it found to calculate its answer—and if its training was good, it’ll get it right most of the time.
Conveniently, this function approximation process is what we need to solve a PDE. We’re ultimately trying to find a function that best describes, say, the motion of air particles over physical space and time.
Now here’s the crux of the paper. Neural networks are usually trained to approximate functions between inputs and outputs defined in Euclidean space, your classic graph with x, y, and z axes. But this time, the researchers decided to define the inputs and outputs in Fourier space, which is a special type of graph for plotting wave frequencies. The intuition that they drew upon from work in other fields, says Anima Anandkumar, a Caltech professor who oversaw the research, is that something like the motion of air can actually be described as a combination of wave frequencies. The general direction of the wind at a macro level is like a low frequency with very long, lethargic waves, while the little eddies that form at the micro level are like high frequencies with very short and rapid ones.
Why does this matter? Because it’s far easier to approximate a Fourier function in Fourier space than to wrangle with PDEs in Euclidean space, which greatly simplifies the neural network’s job. Cue major accuracy and efficiency gains: in addition to its huge speed advantage over traditional methods, their technique achieves a 30% lower error rate when solving Navier-Stokes than previous deep-learning methods.
The whole thing is extremely clever, and also makes the method more generalizable. Previous deep-learning methods had to be trained separately for every type of fluid, whereas this one only needs to be trained once to handle all of them, as confirmed by the researchers’ experiments. Though they haven’t yet tried extending this to other examples, it should also be able to handle every earth composition when solving PDEs related to seismic activity, or every material type when solving PDEs related to thermal conductivity.
Super-simulation
Anandkumar and the lead author of the paper, Zongyi Li, a PhD student in her lab, didn’t do this research just for the theoretical fun of it. They want to bring AI to more scientific disciplines. It was through talking to various collaborators in climate science, seismology, and materials science that Anandkumar first decided to tackle the PDE challenge with her students. They’re now working to put their method into practice with other researchers at Caltech and the Lawrence Berkeley National Laboratory.
One research topic Anandkumar is particularly excited about: climate change. Navier-Stokes isn’t just good at modeling air turbulence; it’s also used to model weather patterns. “Having good, fine-grained weather predictions on a global scale is such a challenging problem,” she says, “and even on the biggest supercomputers, we can’t do it at a global scale today. So if we can use these methods to speed up the entire pipeline, that would be tremendously impactful.”
There are also many, many more applications, she adds. “In that sense, the sky’s the limit, since we have a general way to speed up all these applications.”
from MIT Technology Review https://ift.tt/31XXdy7
Comments
Post a Comment